- Describe the 30* triangle : the 30 degree triangle has and angle of 30 degrees with a radiouse of 1
- Describe the 45* triangle: this trangle has two of the same sides
- Describe the 60* triangle: this triangle is like the opposite of the 30 degree triangle
- How does this activity help you to derive the Unit Circle?this activities help me see the conection with in the unit cirlce and acutally understanding how they get each set of plots for each.
- What quadrant does the triangle drawn in this activity lie in? How do the values change if you draw the triangles in Quadrant II, III, or IV? Re-draw the three triangles, but this time put one of the triangles in Quadrant II, one in Quadrant III, and one in Quadrant IV. Label them as you did in the activity and describe the changes that occur.i kinda forgot because i dotn have the activity anymore
- The coolest thing I learned from this activity was that how the cricles are a bunch of trangles
- This activity will help me in this unit because it make me memorize more clearly how the circle works
- Something I never realized before about special right triangles and the unit circle is the they conect and that how easy it is
megatruong
Thursday, June 5, 2014
I/D 1 unit N
WPP 12 : unit O concept 10
As a helicopter is flying over the afican savanha for animals to catch for a zoo it finds a zebra. The helicopter is flying 40 feet up in the air and the angle a with the dart gun is to the zebra is 50 degrees. how far will the dart go to hit the zebra ?
when the zebra go to the zoo he looked at the people. he looked at a 30 degree angle up to the people. the plat form is 20 feet high of the ground. how far is the new zebra from the plat form ?
when the zebra go to the zoo he looked at the people. he looked at a 30 degree angle up to the people. the plat form is 20 feet high of the ground. how far is the new zebra from the plat form ?
Tuesday, May 20, 2014
Unit U BQ 6
1. What is continuity? What is discontinuity ?
A continuity is when you can draw a graph with out and holes, jumps, unbounded behavior like shown in the second picture.
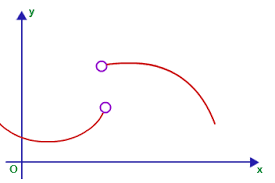
A discontinuity is when you have a graph with jumps , holes, or unbounded behavior. Like in the first picture it is s jump with holes.
2 What is a limit? When does a limit exist? when does a limit not exist? what is the difference between a value and limit ?
A limit is when you plug in x in to the equation.
A limit exist when two things have the same point.
A limit does not exist when they end up at different points like picture 1
A limit is not always on the graph but its what you expect. a value is what your really looking for.
3 How do we evaluate limits numerically, graphically, and algebraically ?
solving limits numerically is very easy. first you need to draw a table with 14 squares in two rows. on the top 7 rows you want to write down the values that you will be plug in to the equation.to find the answers.so solve it graphically we want to the limits. so we look at the graph and determan where everything is by looking at the points and derection of the graph. To solve it algebraically you have three ways of finding them. first is the substitution method witch is when you plug in 0 and see what you get. you can eather get a number , zero, undefined , there is also the factoring method witch simplifyes the equation and then use substitution method agian. and there is also the last one witch is conjugate is when you times it by the conjugate so it simplifies out.


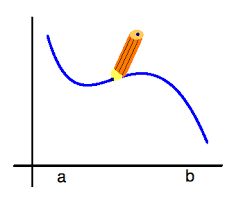
A continuity is when you can draw a graph with out and holes, jumps, unbounded behavior like shown in the second picture.
A discontinuity is when you have a graph with jumps , holes, or unbounded behavior. Like in the first picture it is s jump with holes.
2 What is a limit? When does a limit exist? when does a limit not exist? what is the difference between a value and limit ?
A limit is when you plug in x in to the equation.
A limit exist when two things have the same point.
A limit does not exist when they end up at different points like picture 1
A limit is not always on the graph but its what you expect. a value is what your really looking for.
3 How do we evaluate limits numerically, graphically, and algebraically ?
solving limits numerically is very easy. first you need to draw a table with 14 squares in two rows. on the top 7 rows you want to write down the values that you will be plug in to the equation.to find the answers.so solve it graphically we want to the limits. so we look at the graph and determan where everything is by looking at the points and derection of the graph. To solve it algebraically you have three ways of finding them. first is the substitution method witch is when you plug in 0 and see what you get. you can eather get a number , zero, undefined , there is also the factoring method witch simplifyes the equation and then use substitution method agian. and there is also the last one witch is conjugate is when you times it by the conjugate so it simplifies out.




Monday, April 21, 2014
BQ#3 unit t
how do the graphs of sine and cosine relate to each of the others ?
tangent is like an inverse of a sine and cosine.
cotangent it uses the base of sin and cosine but in this one it has two parts of the graph
secant it is when ever cosine equal to zero and it looks like a parabola
cosecant when ever sine is zero and it has two asymptotes
tangent is like an inverse of a sine and cosine.
cotangent it uses the base of sin and cosine but in this one it has two parts of the graph
secant it is when ever cosine equal to zero and it looks like a parabola
cosecant when ever sine is zero and it has two asymptotes
BQ#5 unit T concept 1-3
5 Why do sine and cosine not have asymptotes, but the other four graphs do?
Both sine & cosine cycle past the value 0, therefore secant & cosecant approach 1/0, which isn't allowed mathematically. It is at this value you will find the asymptotes.
Both sine & cosine cycle past the value 0, therefore secant & cosecant approach 1/0, which isn't allowed mathematically. It is at this value you will find the asymptotes.
Friday, April 18, 2014
BQ #4 unit t concept
3 Why is a "normal" tangent graph uphill, but a "normal" tangent down hill?
There are parts of a graph that will slope down but after it reaches the center it turns 180 degrees and goes to the opposite direction. its like the unit circle when open the the fan and that sewwt lile
There are parts of a graph that will slope down but after it reaches the center it turns 180 degrees and goes to the opposite direction. its like the unit circle when open the the fan and that sewwt lile
Wednesday, April 16, 2014
BQ #2 unit T
What is a period ?
A period is a set of repeating graphs
Why is the period for sin and cosine 2 pie ?
It is because when graphing it the quadrants are different in sin and cosine have the negative on the same side as the other negatives and some with positives. it needs to go threw one whole round of it for a graph to finish.
What is amplitude ?
it is what number that will determine how far your graph will go up.
Why does sin and cosine have amplitudes of 1?
as you see in the unite circle we see that sin and cosine both have the hypotenuse in its equation and on the unit circle that hypotenuse is always one no matter what.
A period is a set of repeating graphs
Why is the period for sin and cosine 2 pie ?
It is because when graphing it the quadrants are different in sin and cosine have the negative on the same side as the other negatives and some with positives. it needs to go threw one whole round of it for a graph to finish.
What is amplitude ?
it is what number that will determine how far your graph will go up.
Why does sin and cosine have amplitudes of 1?
as you see in the unite circle we see that sin and cosine both have the hypotenuse in its equation and on the unit circle that hypotenuse is always one no matter what.
Subscribe to:
Posts (Atom)

