RWA #1 Unit M Concept 5 elipses

RWA #1 Unit M Concept 5 elipses

1. Ellipse - The set of all points such that the sum of the distance from two points is a constant. 

The ellipse 

f

http://www.sparknotes.com/testprep/books/sat2/math2c/chapter8section4.rhtml

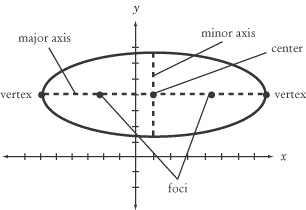
2.  To find the ellipse it has to be in standard conic form which is (x-h)^2/a^2+ (y-k)^2/b^2 = 1. It doesn't matter in what order a^2 and b^2 are they can be under whichever equation. h and k have to be in a specific one. H always has to be with x and k always has to be with y. another thing is that to determine the size of the ellipse if it's skinny or fat has to be based on x or y. If there ia a bigger number under x then it's fat, but if it's under the y then it's skinny. As you can see on the picture whatever d and d 2 are when they are added they equal 2a. 
    When graphed h,k will be center points. What ever numbers are on the bottom like we said then it  place will be a and the second one b.vertices come from a, co-vertices from b, and foci from c and we find c from a^2-b^2=c^2. If a has bigger numbers then it's our major axis and b will be minor axis. The foci will be on the major axis but a little before the vertices points. To determine the eccentricity of an ellipse,is e = c/a. So it's whatever number is c comes out to be divided by whatever number a is. 

http://www.youtube.com/watch?v=-OPR7Krjj7c

3.A great example for and an ellipse would be a chain on a bicycle. As your feet move on the handle . The hardest part or the part where its the  is the parking a lot.  and the chain is the circle that keep revolving 

4.

1  http://www.sparknotes.com/testprep/books/sat2/math2c/chapter8section4.rhtml
2  http://www.youtube.com/watch?v=-OPR7Krjj7c
3  http://mathforum.org/library/drmath/view/62576.html

SP#6 : UNIT k concept 10 Writing a repeated decimal as a rational number using geometric series

the trickiest part about these kind of problems are when there is a number infront of the decimal. when you do it make sure you keep it neat because you can mess this up very easily.

Fibonacci haiku: The Platypus

Duck

Beaver

Whats that

Something very weird 

What could this thing be 

This strange animal could exist as a platypus

SV# 1: Unit F Concept 10: Finding all real and imaginary zeroes of a polynomial

for the video click here
The tricky parts of this kind of problems are the negative values. You have to make sure you are putting then in the right place and make sure you keep track of your negatives. Also the ones that cant be factored all the way are tricky too. You have to use the quadratic equation.

SV #2 Unit G : Concpets 1-7 : Finding all parts and graphing a rational function

to watch my video click here 

the difficalt parts about the problem are the division part you cant make a mistake. also finding the limited notations in the graph are dificult. for me graphin was the hardest part for me. i didnt really understand what parts go where. 

SV3:Unit H Concept 7 - Finding Logs Given Approximations

To watch my SV3 click here 
For this problem you will need to watch out for some small things. First is the when a log is equal to 1 .  you should already know that but some times it slips. Also when you bring up the numbers on the bottom of the fraction all your doing is adding negative to them and boom your done. You need to make sure you factored the problem corectly and there are more then one way to factor it out. So if you have a diffrent answer then dont worry you both are right. Thats all i have to say for this concept >

SV4: Unit I Concept 2- Graphing logarithmic equations

Please see my video by clicking here.

The hardest part of this equations are the y- intercepts. you have to set the logs to equal each other, and also another tricky part is when you graph it on a calculator. It does not go all the and dose not show the x intercept for the domain. If you are use to normal equations then the domain and range are switch for good reasons.